Solving Equations for Physical Understanding
Introduction
I have been teaching undergraduate aerospace and mechanical engineering students and physics students for more than 20 years. In that time I have made and heard others make complaints that our students are not comfortable with mathematics and that this problem is getting worse with time, particularly in dealing with the differential equations (D.E.s) that show up all the time in engineering problems. I suspect that teachers have always made such statements to a greater or lesser extent, at least partially because we forget how many mistakes we made when we first started learning to be engineers. Or perhaps some of it is because the people who teach engineering are drawn from the top cohort of engineering students, and only learn about the continuum of talent in undergraduate courses when they are asked to teach them. But there also seems to be some evidence to suggest that students are having more difficulties now than previously with mathematics, particularly for the more advanced topics like the use of D.E.s.
I can blame the internet, of course — students have difficulty with finding time for the pen-and-paper practice that is required to achieve facility with and understanding of the mechanics of basic mathematical techniques like differentiation and integration because students have many more (and many more fun) things they (could/should/must/would like to) do on a computer.
But if I am honest with myself, and look back through the mists of time, I was not so hot at this process myself when I was an undergraduate student, and I didn’t have the distractions that our current generation of students have.
So what causes this problem and how do we solve it? My working hypothesis is that at least some of the problems arise from not linking the mechanics of the mathematics with our physical experience. Students learn mathematics as an abstract set of tools for solving equations, and then we expect them to use those tools to solve physical equations without linking the equation(s) to the students’ intuitive understanding of the physics of the problem systematically: many students treat the problem and its mathematical solution as two completely separate and unrelated problems.
In the particular case of aerospace engineering, this experience is encapsulated by a student being repeatedly exposed to the Navier-Stokes equations, a set of formidable partial differential equations that can describe most fluid-dynamical problems but can only be solved analytically in a few simple cases. We explain those cases and students dutifully copy down the methods and repeat them to us in exams at the end of the term, if we and they are lucky.
Now the Navier-Stokes equations are wonderful, but they are difficult to understand for most engineering students because they are so general and so very nonlinear. The pedagogical principle that we follow in aerospace engineering seems to be that if you show these equations to students frequently enough they will eventually `stick’ through repetition and familiarity. So we keep exposing the students to these equations and how they can be manipulated into more immediately useful simplified forms until something magical happens and the student starts to understand how to use them. For the best students, this is the case, but many more students get by on memorising specifics sufficiently well to get through the exams, never really coming to terms with what the equations mean physically and how they can be simplified.
The approach to engineering mathematics education I’ve just mentioned is equivalent to a magician telling a new apprentice to read a book on how to saw their assistant in half, follow the instruction and perform the trick. It’s a process more likely to result in a lot of bisected assistants and a very dispirited apprentice magician than it is to produce a successful magic trick.
Of course those who have a good understanding of the Navier-Stokes equations have the ability to solve a wide range of problems in fluid mechanics by going from the general problem to specific cases of interest, making the right sorts of simplifications at the right times. This is what we would like our students to be able to do. But this ambition is very difficult to achieve when you are learning, and so it seems to me that a better approach involves solving simpler problems and working your way up to the more difficult ones as you gain experience. If the simpler problems are chosen carefully, you can teach the basic ideas without the complications that make understanding the concepts unnecessarily difficult.
In terms of our magician analogy, it would seem more sensible to teach a simpler and less frustrating trick, like pulling a rabbit out of a hat (I don’t know if this is actually less simple than sawing an assistant in half, but let’s assume it is, because the process is reversible if you get it wrong, unlike sawing someone in half). One might start with a stuffed rabbit and a top hat and go through the process several times, eventually getting the student to try it independently and with a live rabbit. Then perhaps teach them how to do the same thing with a chef’s hat or a sombrero … until the student realises that they are all just hats and that the type of hat does not change the trick — the hats are all just hats.
For differential equations, the equivalent to learning magic this way is to solve different first-order D.E.s describing different problems. Not initially as a purely mathematical exercise, but by some kind of approximate method that makes use of the student’s physical intuition and their understanding of the problem. Once this method is determined, the more precise problem can be tackled mathematically with some knowledge of what the solution should look like and why.
The sort of thing that might work well is described in the excellent book “Solving equations with physical understanding” by J.R. Acton and P.T. Squire: ISBN 978-0852747995. Unfortunately the book now appears to be out of print. It details a method for the approximate solution of ordinary and partial differential equations that relies on the physical behaviour of the problem rather than on the mathematical techniques involved in the direct solution of the D.E. You could think of it as a `back of the envelope’ solution for differential equations that provides physical insight about the meaning of the solution to the D.E. By tackling simple differential equation problems with this method and then doing the same thing more formally, we can consciously combine our physical intuition about the behaviour of the differential equation with our mathematical understanding of its solution. This helps bridge the gap between a purely mathematical understanding of differential equations and the ability to use D.E.s to sqolve new engineering problems from scratch, which should ultimately be our aim in looking at these equations in the first place. By solving many of these simple problems in a range of domains, engineering students are able to develop their ability to recognise the fact that, like the magician’s apprentice, for many of these problems although the hats look different, they are all just hats.
To give an example, after this too-long introduction, I’ll reproduce the first example used in the book, involving a familiar physical problem that involves solving a first-order differential equation. We will take the equation, make a qualitative sketch (QS) of the functional form that the solution should take, using our physical understanding of the problem. Then we will substitute that test function (TF) into the equation to determine a model for the physical behaviour. Then, because the problem is simple enough, we will compare the approximate solution obtained through this process (called in the book the QSTF process) with the actual solution obtained by solving the differential equation.
Exponential Growth and Decay
Many problems involve an exponential-shaped growth or decay from an initial value that is fixed to gradually rise or fall until it very closely approaches a final value, which mathematicians refer to as an asymptotic approach to that value that, like Achilles in Zeno’s paradox of his race with the tortoise, never quite gets to that final value. As an example of an exponential decay, Fig. 1 shows three plotted decay curves starting from a value of \(u_0\) at \(t = 0\) changing asymptotically to zero with three different time constants.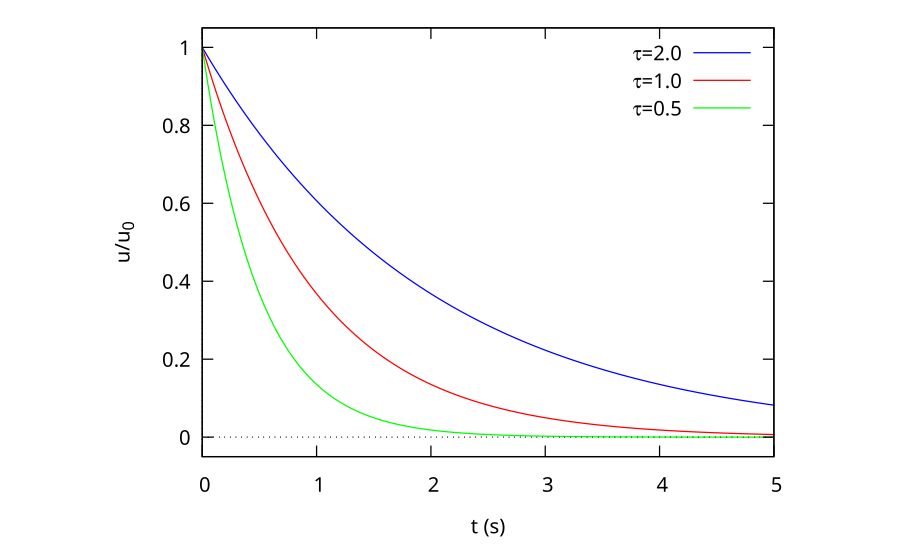
Figure 1: Exponential decay curves for 3 time constants
Other problems will involve an exponential rise from zero to an asymptotic limit, and can be described by the equation
\begin{equation}
\label{orgac57ec5}
u = u_\infty(1 – e^{-t/\tau})
\end{equation}
As a plot, this looks like Fig. 2
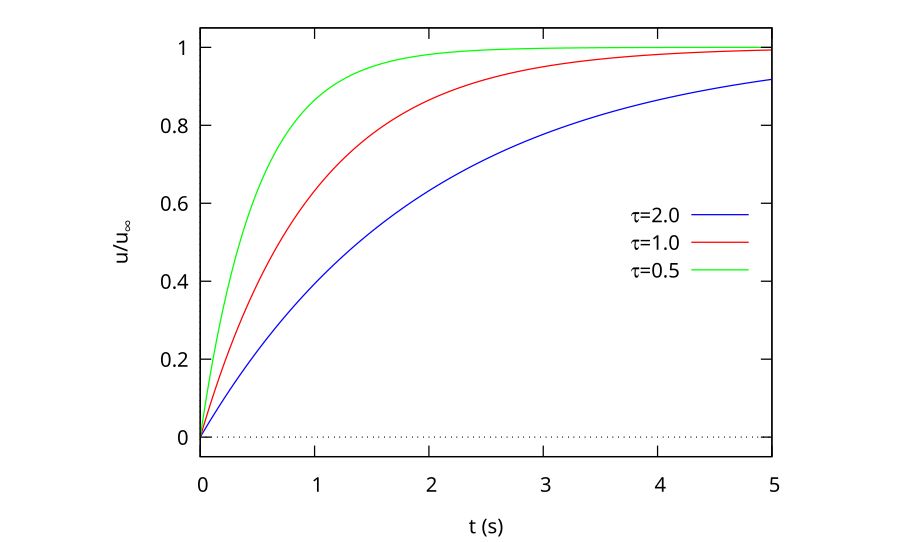
Figure 2: Exponential rise curves for 3 time constants
The most general case of a smooth exponential transition between two non-zero states \(u_0\) and \(u_\infty\) is described by
\begin{equation}
\label{org7a2ccea}
u = u_\infty + (u_0 – u_\infty) e^{-t/\tau}
\end{equation}
Why is the Exponential Form so Important?
As we shall soon see, there are other possible functional forms than Eq. \eqref{org7a2ccea} that we could have chosen that have a similar asymptotic growth or decay behaviour with time. But there is a significant advantage to the natural exponential form because the natural exponential’s derivative is the same as that of the original function, i.e.
\begin{equation}
\frac{d}{dx} e^x = e^x
\end{equation}
or is a constant factor times that function, like
\begin{equation}
\frac{d}{dt} e^{-t/\tau} = -\frac{1}{\tau} e^{-t/\tau}
\end{equation}
This means that the behaviour with time can be described using a single characteristic time parameter, \(\tau\). The physical meaning is that when t = \(\tau\), the solution will have changed by (1 – e^{-1}) = 63.2 per cent of the total change, and every subsequent \(\tau\) will be 63.2 per cent of the remaining change (i.e. 63.2 per cent of 36.8 per cent etc.).
Example: a Falling Rock
Consider the case of a rock falling under the influence of gravity and air drag. The differential equation that describes this behaviour is
\begin{equation}
\label{org885b28d}
m \frac{dv}{dt} = mg – bv^2
\end{equation}
\begin{equation}
[mass \times acceleration] = [gravity force – air drag]
\end{equation}
where \(b\) is the drag coefficient of the body, determined by its shape.
If dropped with an initial velocity of zero, the rock should increase its speed smoothly from zero until reaching a constant velocity when the forces balance, i.e. when
\begin{equation}
mg = bv^2
\end{equation}
or
\begin{equation}
v_\infty = \sqrt{\frac{mg}{b}}
\end{equation}
Although there are a number of ways in which the object could reach the final velocity, the simplest one associated with the gradual balancing of two forces might look like one of those in Fig. 2, with the time constant determined by the mass, the gravitational force and the drag coefficient of the object.
As an aside, notice how in the discussion above I snuck in the assumption that the drag was proportional to the square of the velocity of the object? In fact, this is only true at higher Reynolds numbers and the drag force would be linearly related to velocity at lower speeds. This is one of the dangerous aspects of treating the equation as being independent of the physical problem to be solved. Although the rock would need to be physically very small to have a low enough Re to be proportional to the velocity, I have still seen this form in several example problems in maths textbooks.
While the D.E. in Eq. 5 can be solved directly, we will find an approximate solution using our physical understanding of the problem. This involves 3 basic steps:
- making a qualitative sketch (QS) of the solution (we have done this already in Fig. 2)
- using this sketch to make a trial function (TF) that describes the equation;
- using the TF to determine a design formula for the time constant of the exponential rise
Qualitative Sketch
There are a number of possible ways in which the stone’s velocity can fall as a function of time. Four possibilities are shown in Fig. 3, labelled A through D. Curve A has an overshoot in velocity before reaching a steady value. This sort of thing might happen in an active control system if there is a lag between the controlling force being applied and the effect it has on the speed, but this does not seem likely in the case of air resistance, where the effect is very quick. Curve B has a discontinuity, and does not seem physically realistic. Curve C is smooth and reaches the asymptotic value gradually, so looks like something that would happen. Curve D has a saddle point, and we can’t easily find a reason for that to happen, so it looks like curve C, our exponential growth equation from Eq. \eqref{orgac57ec5}, is the correct functional form.
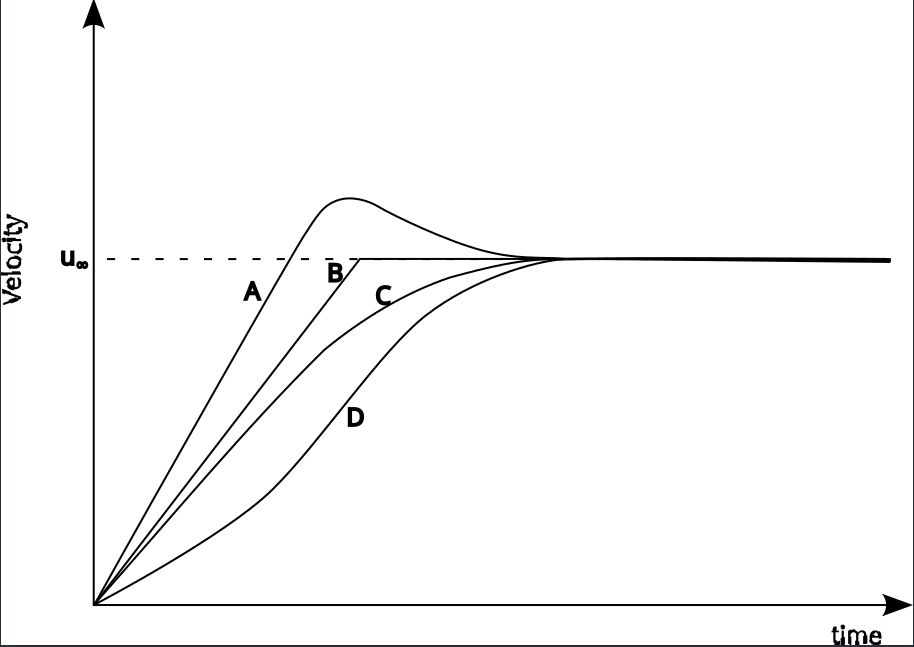
Figure 3: Possible sketches of falling stone velocity
So we are going to assume that this is the general form for the behaviour of the falling stone. Now it may or may not be the exact form, but it has the general behaviour expected of the physical phenomenon. If the equation form is not correct, we can still deduce a time constant that we feel should be reasonably close to the exact time constant.
Trial Function
We choose as the trial function
\begin{equation}
\label{org9876284}
v^* = v_\infty (1 – e^{-t/\tau})
\end{equation}
Here the asterisk indicates that this is a trial function rather than the correct functional description for the behaviour.
Estimating the Time Constant
To get an equivalent time constant, we must substitute our test function Eq. 9 into the differential equation Eq. 5. The derivative is
\begin{equation}
\frac{d v^*}{dt} = \frac{V_\infty}{\tau}e^{-t/\tau}
\end{equation}
and
\begin{equation}
\begin{aligned}
m \frac{dv^*}{dt} &= mg – b v^{*2} \\
m \frac{v_\infty}{\tau} e^{-t/\tau} &= mg – b \left[v_\infty \left( 1 – e ^{-t/\tau}\right) \right]^2 \\
\frac{v_\infty}{\tau} e^{-t/\tau} &= g – g \left( 1 – e^{-t/\tau}\right)^2
\end{aligned}
\end{equation}
Because this is only an approximate solution, there will be a residual \(\mathcal{R}\) relative to the `proper’ solution, which is expressed in terms of the solution’s difference compared with the actual solution:
\begin{equation}
\frac{v_\infty}{\tau} e^{-t/\tau} = g – g \left( 1 – e^{-t/\tau}\right)^2 + \mathcal{R}
\end{equation}
or
\begin{equation}
\label{org68c7fed}
\mathcal{R} = \frac{v_\infty}{\tau} e^{-t/\tau} – g + g \left( 1 – e^{-t/\tau}\right)^2
\end{equation}
The value of \mathcal{R} varies with both the independent variable \(t\) and the time constant \(\tau\). This means we can only force the residual to be zero at certain values of \(t\). If we could make \( \mathcal{R} = 0\) for all values of \(t\), then we would have the correct test function, which is not generally going to be the case.
Collocation at the Half-Way Point
Generally speaking, we want to fix our solution at a point that maintains a good agreement with the actual solution over as much of the solution domain as possible. As the exponential rises from 0 to 1 at \(t = 0\) and \(t = \infty\) respectively, then it makes sense to tie our approximate solution to the actual solution (a method called collocation in the book) at \( e^{-t/\tau} = 0.5\). We do this by setting \( \mathcal{R} = 0\) at this point.
So Eq. 13 becomes
\begin{equation}
\begin{aligned}
\frac{v_\infty}{2\tau} & = g – g (1 – 0.5)^2 \\
& = \frac{3g}{4}
\end{aligned}
\end{equation}
so
\begin{equation}
\label{org7c393cf}
\begin{aligned}
\tau & = \frac{2 v_\infty}{3g} \\
& = \frac{2}{3g} \sqrt{\frac{mg}{b}} \\
& = \frac{2}{3} \sqrt{\frac{m}{gb}}
\end{aligned}
\end{equation}
and the final form of the approximate solution can be determined by substituting for \(\tau\) into Eq. 15:
\begin{equation}
v^* = v_\infty \left(1 – e^{\frac{-t}{\frac{2}{3}\sqrt{\frac{m}{gb}}}}\right)
\end{equation}
Note that in doing this we are not directly solving the differential equation expressed in Eq. 5. We are determining an approximate solution to an equivalent exponential rise problem which will have a very similar time constant. As the time constant is the useful part of the solution, this is really all we need. We are not as concerned with the mathematical correctness of the solution as we are with the physical usefulness.
Note that we didn’t have to collocate at the half-way point. We could have got a different time constant by collocating either earlier or later in the process. The best value across the domain will be the collocation at the half-way point, but if you want a better solution close to \( t = 0\) then you might want to collocate at 0.2 instead, for example. Note that one way of determining how well you have approximated the exact solution to the problem is to determine the collocation at the 0.2 and the 0.8 mark as well as the 0.5 mark. If the time constants are within a factor of 2 of one another across this range, it’s a reasonable approximation across the entire domain, for engineering purposes. Because the collocation process is fairly straightforward, determining the time constant in this way can often provide a good engineering solution with a good idea of its accuracy without ever having to solve the differential equation directly. And if you then go on to solve the exact D.E. then you will have the physical understanding of the problem to back up your solution as a bonus.
`Proper’ Solution and Comparison
In the case of a falling stone, you can directly integrate the equation and, armed with some derivative formulas or a table of standard integrals the solution is given by
\begin{equation}
v = \sqrt{\frac{mg}{b}} \tanh \left(\sqrt{\frac{bg}{m}} t\right)
\end{equation}
and from Fig. 4, we can see that the hyperbolic tangent form is not exactly the same as the exponential growth form, so our solution is, indeed, approximate. The general behaviour of the two functions is similar, but the exponential distribution is `fuller’ for the same time constant (\(\tau = 1\) in this case).
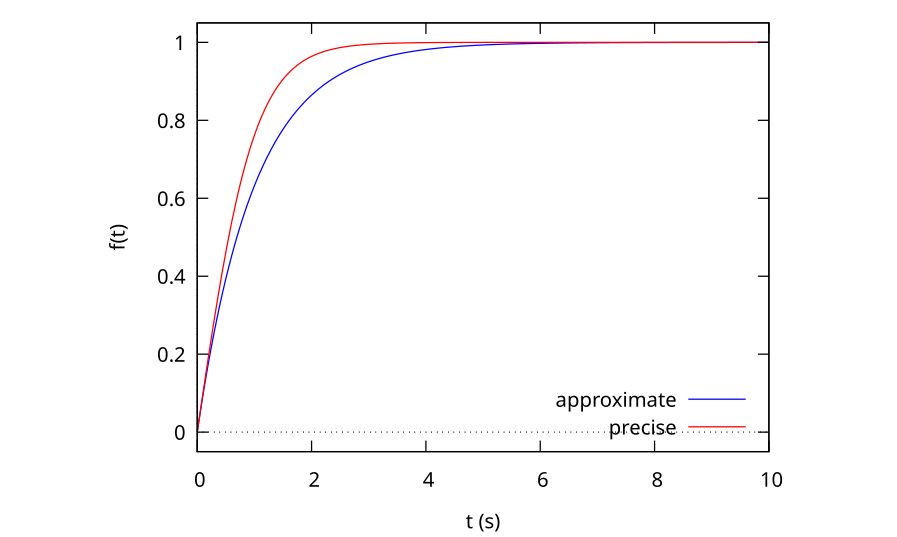
Although the physical process is not exactly an exponential growth, we can still determine an effective time constant from the mathematically correct solution, if it’s defined as the time required to grow to 63 per cent of the full velocity, in an analogous way to the exponential growth problem. When we do this we get
\begin{equation}
\tau = 0.745 \sqrt{\frac{m}{gb}}
\end{equation}
compared with the
\begin{equation}
\tau = 0.67 \sqrt{\frac{m}{gb}}
\end{equation}
obtained in Eq. 15 using our approximate form. This is around 11 per cent higher than the approximate solution, and is well within our acceptable limit of 30 per cent.
To see the difference between the two solutions, we can plot them both as a function of time, as shown in Fig. 4. It is clear that the approximate solution is very close to the precise solution, which is why the time constants are also close. The collocation point is indicated by the crossover of the approximate and precise solutions. As mentioned, we could collocate earlier to get a better fit to the earlier part of the curve or later to be more accurate later in the history.
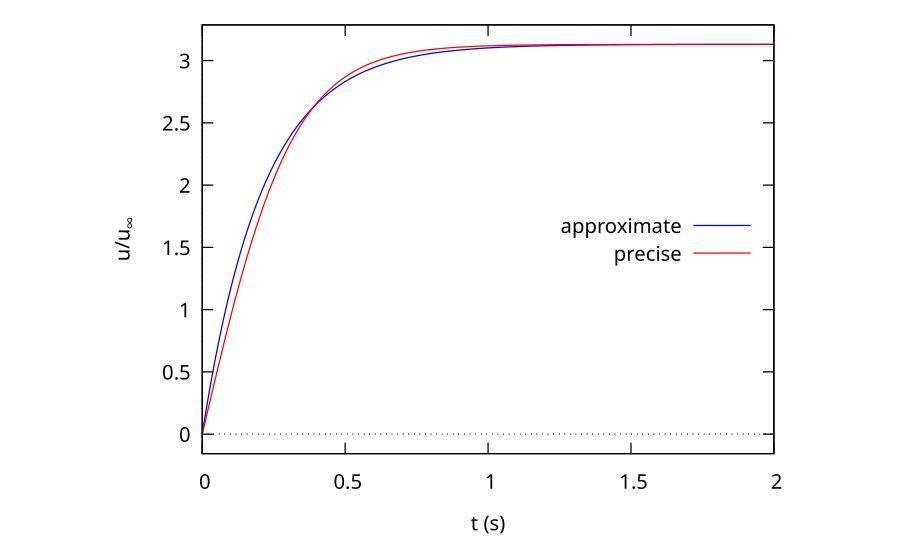
In comparing the approximate solution to the mathematically correct one, we see that we have acquired something valuable in exchange for the small inaccuracy. Now we can express the temporal behaviour of the velocity in terms of a physical time constant that just drops out of the analysis because the exponential form is self-similar in a very similar way to how the boundary layer equation is self-similar. But this problem is a lot easier to understand.
Given that we did not solve any differential equations to achieve this approximate result, the fact that both the time constant and the general shape of the curves are so close is an indication fo the power of the technique in a predictive sense, but I think what’s even more impressive is how helpful such a process is for assisting students to understand the mathematical behaviour of the problem using some fairly straightforward physical observations.