DSMC in J 1
Background & Motivation
Some of my research involves flow having very low densities, or flows of moderate densities in very confined spaces, such as capillary tubes. These flows are known as rarefied flows. Rarefied flows have some interesting properties: in particular, flow can slip past boundaries, whereas at higher densities the flow would have zero velocity at a surface relative to the velocity at that surface (why cars remain dusty even when you drive them fast). In hypersonics, rarefied flows are interesting because as the flow is fast and the density is low, then fluid mechanical or chemical reaction changes can take place over similar time scales as the flow time past the object of interest. This leads to what are called nonequilibrium processes, where time scales can have an important effect on flow or on chemical reaction processes.
The DSMC Method
Because the computational solution of the fluid flow equations that treat fluids as a continuous medium assume no flow slip at surfaces, those models begin to fail when the flow gets rarefied. One very successful method for simulating rarefied flow is the direct simulation Monte Carlo (DSMC) method. This is a statistical model of flow, and was invented in the 1960s by the Australian aeronautical engineer Professor Graham Bird. I was fortunate to meet Professor Bird on several occasions later in his life (he died in 2018) and he was a very inspiring scientist. He continued to make significant contributions to rarefied flows right up to the end of his life.
DSMC is a fairly straightforward simulation method based upon a statistical treatment of collisions in rarefied gases, and because it models collisions with walls, then the slip phenomenon automatically drops out of the simulation, provided the modelling of collisions of gas atoms or molecules with the wall are physically correct. Now the most obvious way to simulate the flow of a low density gas using a computer would be to keep track of the position and momentum of every nitrogen and oxygen molecule in an air flow, step forwards in time in very small increments, calculates trajectories for each molecule during this time step to determine whether individual molecules collide with each other or with surfaces and then implement some sort of model (like Newton’s laws) for how energy and momentum are transferred for whatever collisions that occur during the time step. This idea is called Molecular Dynamics (MD). It is very useful because of its simplicity and the transparency of the physical modelling involved, but it involves too much computation for all but the smallest flow volumes and all but the lowest densities – the flow domain has to be checked at each time step for collisions between each molecule and every other molecules.
DSMC overcomes much of the problems of MD for larger flow volumes by making two very clever assumptions. The first is that the behaviour of very large collections of molecules can be simulated by considering the behaviour of a much smaller number of molecules, appropriately scaled. This alleviates the problem of dealing with astronomical numbers of physical molecules. The second assumption is that on average the behaviour of collisions between molecules can be explained by statistical means based upon knowledge of the relative speeds of the potential collision partners. Thus instead of having to solve the conservation of momentum and energy equations for each collision, the probability of collision and the post-collision trajectories can be calculated using random number generation, with the overall behaviour of the flow averaging out to the correct values. These two assumptions make DSMC capable of accurately simulating rarefied flow behaviour for a range of practical engineering problems.
I will try to explain how I split the problem up and tested the components independently as I go through the design and implementation of DSMC. The implementation will be split among various posts as I go along (and as it’s being done in my spare time, this might take a while), and I’ll discuss how I decided to attempt different solutions that didn’t work, and the struggles to get an elegant and functional loopless code. I’m not an expert in either J or DSMC, just an enthusiastic amateur. But I hope that some people will find it interesting enough to begin their own investigation of this simulation method, or be inspired to take a closer look at the frankly beautiful J programming language.
I teach a very basic version of the DSMC method to my hypersonics class, and this year I asked them to code up a simple solution as an assignment question. For this blog, I thought I would go through my method of implementing the simulation, so that those unfamiliar with molecular simulation may be tempted to try it out. To make the problem more fun for me, and because it’s a good match, I have decided to implement my solution in the J programming language. J is an array-based programming language, created by Kenneth Iverson and descended from APL, the first of the array-based languages. I chose J because, being an array-based language, it is very well suited to operation on arrays of large numbers of particles that are all doing similar things. Given that very few people know the J language, and that the intersection of those who are interested in J and are interested in DSMC has probably only one member (me) then this can be seen either as a tutorial for the J programming language that uses DSMC as an example application, or an explanation of simple DSMC that uses J as a method for describing the algorithms. My other goal in putting this together was to see if I could write some nice functional code in J that helps me cement my understanding of the DSMC method.
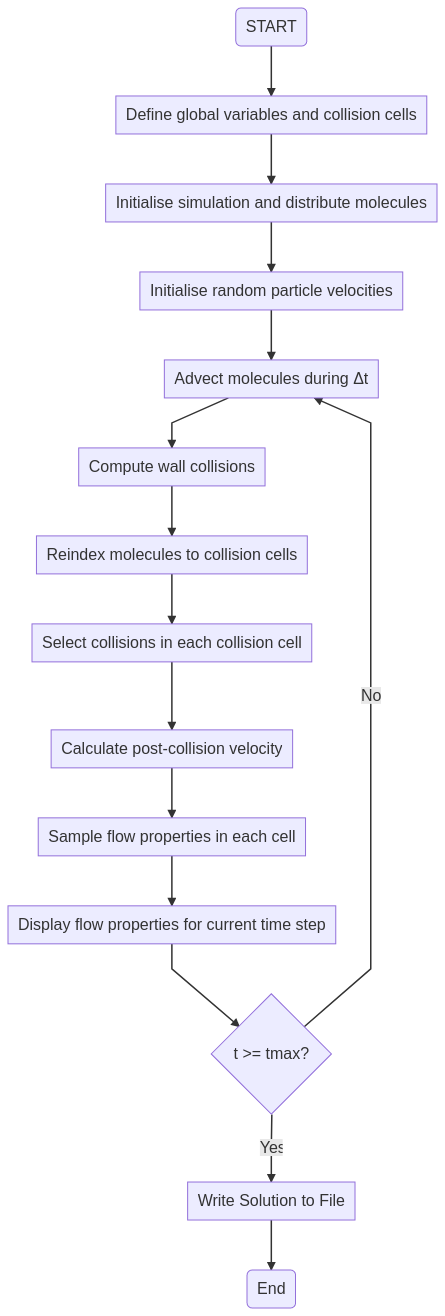
Figure 1: DSMC Flowchart
The flowchart in Fig. 1 shows the algorithm at its simplest. A representative set of molecules is uniformly distributed across the flowfield, with randomised thermal velocities superimposed upon a bulk velocity. The thermal velocities are determined using a Boltzmann distribution as a function of the initial temperature of the gas. The flowfield itself is broken up into a group of collision cells that can be of arbitrary shape or size, with a fixed number of particles within the cell. The size of the cell is therefore dependent on the local density of the flow. These particles (which I will, for convenience, call molecules regardless of whether they are molecules or atoms) are each representative of millions to billions of actual particles in the flow. A very small time step, which depends on the size of the cell, is used to determine the motion of the molecules and, along with the relative velocities of pairs of molecules, the probability of collisions. Collisions with walls and with other molecules are simulated, and the particles are re-assigned to their new cells if they move from one cell to another. After this movement, the velocities of the particles in each cell are used to determine the flow properties in the cell, and the time is incremented by Δt again. This continues until either the flow has reached a steady state or a pre-assigned time has elapsed, at which point the code stops.
As Fig. 1 and the description above indicates, the DSMC algorithm at heart is not complicated, although it should be pointed out that state-of-the-art DSMC implementations have many improvements to this simple model, to ensure that the code runs quickly and that cells or simulations are parallelised. Some real DSMC codes that you can download and use include Bird’s DS2V code or Michael Gallis’ SPARTA code, amongst others. I mention these ones specifically because they are directly downloadable so you can play with them.
There is a lot of information available in books about the DSMC method. Some references that you should look at include Prof. Bird’s original text bird1995molecular and his more recent implementation book bird2013dsmc. Other more recent texts that cover the DSMC algorithm include those by Sharipov sharipov2015rarefied and by Boyd and Schwartzentruber boyd2017nonequilibrium. We have used DSMC for validation of a number of hypersonic separated flow configurations. Some references to this work include gai2019large, le2019rotational, prakash2018direct and hruschka2011comparison.
Most of the textbooks mentioned above contain a fair amount of kinetic theory, because there is a lot of physics to be considered when dealing with collisions of molecules with each other and with surfaces. For the purposes of explaining the process of the DSMC algorithm, that extra detail is not necessary. Instead, I have used the paper by Alexander and Garcia alexander1997direct as the model for the DSMC method used here. The paper itself can be found on Prof. Alejandro Garcia’s web site (Paper), along with a lot of other interesting simulation papers. He has also written a book on numerical methods in physics which has one chapter dedicated to implementation of DSMC in Matlab or Python (or C++ or Fortran) if you prefer to avoid J or my explanations.
Over time on this blog, the plan is to implement a simple DSMC simulation in J of the flow of low density gas through a heated capillary tube of square cross-section. Each one or two steps in Fig. 1 will be implemented and described in individual blog posts, building up to the final program.
Bibliography
- [bird1995molecular] Bird, Molecular gas dynamics and the direct simulation of gas flows, Oxford, United Kingdom: Clarendon Press(Oxford Engineering Science Series,, (42), (1995).
- [bird2013dsmc] Bird, The DSMC method, CreateSpace Independent Publishing Platform (2013).
- [sharipov2015rarefied] Sharipov, Rarefied gas dynamics: fundamentals for research and practice, John Wiley & Sons (2015).
- [boyd2017nonequilibrium] Boyd & Schwartzentruber, Nonequilibrium Gas Dynamics and Molecular Simulation, Cambridge University Press (2017).
- [gai2019large] Gai, Prakash, Khraibut, Le Page & O’Byrne, Large scale hypersonic separated flows at moderate Reynolds numbers and moderate density, 100005, in in: AIP Conference Proceedings, edited by (2019)
- [le2019rotational] Le Page, Barrett, O’Byrne & Gai, Rotational temperature imaging of a leading-edge separation in hypervelocity flow, 110001, in in: AIP Conference Proceedings, edited by (2019)
- [prakash2018direct] Prakash, Gai & O’Byrne, A direct simulation Monte Carlo study of hypersonic leading-edge separation with rarefaction effects, Physics of Fluids, 30(6), 063602 (2018).
- [hruschka2011comparison] Hruschka, O’Byrne & Kleine, Comparison of velocity and temperature measurements with simulations in a hypersonic wake flow, Experiments in fluids, 51(2), 407-421 (2011).
- [alexander1997direct] Alexander & Garcia, The direct simulation Monte Carlo method, Computers in Physics, 11(6), 588-593 (1997).
Leave a Reply